Математические основы kNN

В этой статье будет рассмотрен один из примеров применения нейронных сетей в автоматической торговле, а именно метрический классификатор k-ближайших соседей. Мы постараемся наиболее полно описать этот алгоритм, причём все математические тонкости пояснить наиболее просто, чтобы всем было понятно.

Математическая часть классификатора.

Этот раздел статьи очень важен для дальнейшего понимания материала, поэтому отнеситесь к нему серьёзно. Всем кто «дружит» с математикой можно пропустить этот раздел, чтобы не терять время.

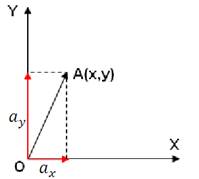Вектор – это направленный отрезок в пространстве(на плоскости). У вектора есть две характеристики: длина и направление, но мы будем рассматривать вектора немного по-другому. Ниже представлена декартова система координат, всем знакомая ещё со школы. На этой двумерной системе координат отмечен вектор А, с координатами x и y. x – расстояние откладываемое по оси OX, аналогично y - расстояние откладываемое по оси OY. Таким образом, у вектора есть две координаты которые указывают конец вектора. Начало вектора находиться в нулевой системы координат. При условии если начало вектора будет в нулевой точке системы координат, то длинна вектора считается по формуле |a| = .

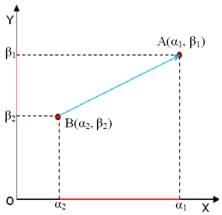Теперь рассмотрим две точки в декартовой системе координат. Точка А(?₁, ?₁) и В(?₂, ?₂) ? – координаты точек по оси OX, ? – координаты точек по оси OY. Нам нужно найти расстояние между этими 2-я точками. Голубым цветом нарисован вектор длинна которого будет равна расстоянию между точками А и В. Каким образом это связано с нейронными сетями и классификатором? – спросите Вы меня, скажу сразу в математике всегда так, Вы должны абстрагироваться и понять суть метода, а не заучить формулы, только тогда Вы научитесь «прикладывать» математику к жизненным задачам, дальше поймёте зачем мы вычисляли расстояние между точками. Итак, в предыдущем случае начало вектора было в нулевой точке и мы легко могли посчитать его длину. В этом случае что нам мешает перенести систему координат в точку В(?₂, ?₂)? Ничего,  другой вопрос как это сделать. Поочерёдно из каждой координаты по оси OY вычтем ?₂ , тем самым мы «приподнимем» систему координат вверх, координата ?₂ при это занулиться. Теперь повторим действия для координат по оси OX, этим действием мы пододвинем систему координат вправо. Координата ?₂ занулиться и точка В будет совпадать с нулевой точкой 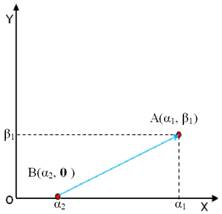системы координат. Теперь по формуле приведённой выше можно легко посчитать расстояние между этими двумя точками. Можно было привести готовую формулу сразу, но тогда Вы не поняли бы суть. Формула по которой можно посчитать расстояние между 2-я точками в двумерной системе координат:  . При работе с классификатором маловероятно то, что Вы будете работать всего лишь с 2-я измерениями. Поэтому стоит привести формулу для расчета расстояния в многомерной системе координат:  , где n это количество измерений.

Основная идея метода классификации k-ближайших соседей.

 Теперь, зная математическую основу классификатора, мы можем перейти к детальному рассмотрению самого алгоритма.

Метрические классификаторы применяются для распознавания образов, они определяют степень «сходства» между различными объектами. Применяются, когда, либо сложно, либо мы не можем сформировать достаточно «хорошее» признаковое описание объектов. Фактически мы используем сырые данные, которые по нашему мнению содержат в себе информацию об объекте, но оснований так считать нет.

Идейная составляющая метрических классификаторов основывается на том, что похожие объекты очень часто находятся «рядом», т.е. на близком расстоянии друг от друга. Для тех кто хочет почитать более строгое основание рекомендую ознакомиться с гипотезой компактности. Рассмотрим, как мы, с человеческой точки зрения, определяем сходство между объектами. Например, как мы распознаём своих знакомых и друзей: мы запоминаем общие черты лица, цвет волос, цвет глаз, голос, походку, стиль одежды и другие признаки. Тех, кого мы видим очень часто, мы просто полностью запоминаем, набор признаков наиболее полон, кого видим реже, запоминаем только общие признаки без деталей. Когда мы получаем информацию от органов восприятия, мы сравниваем её с информацией в памяти, если находиться «схожий» объект в памяти, из памяти сразу же приходит название этого объекта или имя, или все ассоциированные (связанные) с этим объектом воспоминания (информация в памяти). Схожий объект именно по информации, полученной от органов восприятия. Рассмотрим, выше сказанное, на абстрактном примере, который покажет работу метрического классификатора. У нас есть 3 объекта, у каждого из них 2 координаты. Каждый из трёх объектов был замечен (запечатлён в памяти) 5 раз. Чёрным цветом обозначена точку координаты, которой мы знаем, но к какому объекту принадлежит эта точка нужно определить.